Impedanzen messen mit dem Oszilloskop

Mit einem Oszilloskop und einem Messsender lassen sich die Impedanzen elektrischer Bauelemente hochgenau messen. Hierzu wird eine Methode vorgestellt, die Messdaten eines Oszilloskops in einer Tabellenkalkulation wie Excel oder einem statistischen Software-Paket wie R, Python oder Matlab auswertet.

Erstens können mit der hier beschriebenen Methode die Induktivitäten oder Kapazitäten unbekannter Bauelemente ermitteln werden. Weiterhin eignet sich das Verfahren zur Bestimmung von Frequenzgängen, wenn bei hochfrequenten Anwendungen die tatsächlichen Impedanzen stark von theoretischen Werten abweichen. Letzteres ist in der Hochfrequenztechnik ein gängiges Problem, schon weil reale Bauelemente stets verlustbehaftet sind.

Wer mit der Theorie von Blindwiderständen und komplexen Zahlen vertraut ist, kann die folgenden Abschnitte übergehen und direkt beim Versuchsaufbau weiterlesen.

Impedanzen idealer Spulen und Kondensatoren

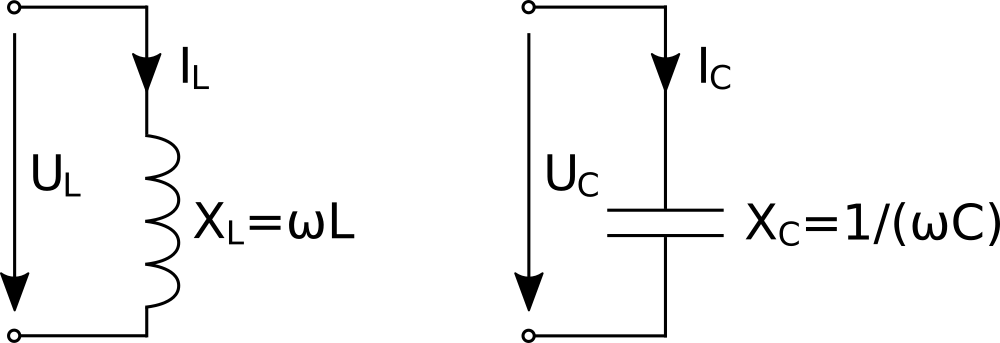
Die Impedanzen idealer Spulen und Kondensatoren folgen aus zwei einfachen Formeln. Aus diesen ergeben sich sowohl XL für Spulen als auch ^X_C für Kondensatoren als Blindwiderstände, was bedeutet, dass Strom und Spannung um 90° phasenverschoben sind.

XL = ω*L
XC = 1/(ω*C)
ω = 2*π*f

L: Induktivität in Henry
C: Kapazität in Farad
f: Frequenz in Hertz
XL: Impedanz der idealen Spule
XC: Impedanz des idealen Kondensators

Bei idealen Spulen eilt die Spannung UL dem Strom IL um 90° voraus und bei idealen Kondensatoren eilt die Spannung UC dem Strom IC um 90° nach.

Aufgrund der 90° Phasenverschiebung verbrauchen Blindwiderstände keine Leistung. Vielmehr speichern diese periodisch Energie, die sie anschließend wieder freigeben.

Sofern bei Impedanzmessungen die Phasenverschiebungen nahe der idealen Werte liegen, lassen sich Kapazitäten und Induktivitäten von Kondensatoren und Spulen auf einfache Weise ermitteln. Hierzu sind lediglich die Beträge von Strömen und Spannungen entlang der Bauelemente zu messen. Anschließend folgen die gesuchten Charakteristiken aus diesen Umrechnungen:

XL = |UL| / |IL|
XC = |UC| / |IC|
L = XL / ω
C = 1 / (ω*XC)

Impedanz realer Spulen und Kondensatoren

In Ersatzschaltbildern realer Spulen und Kondensatoren werden ohmsche Widerstände in Parallel- und Reihenschaltung eingefügt.

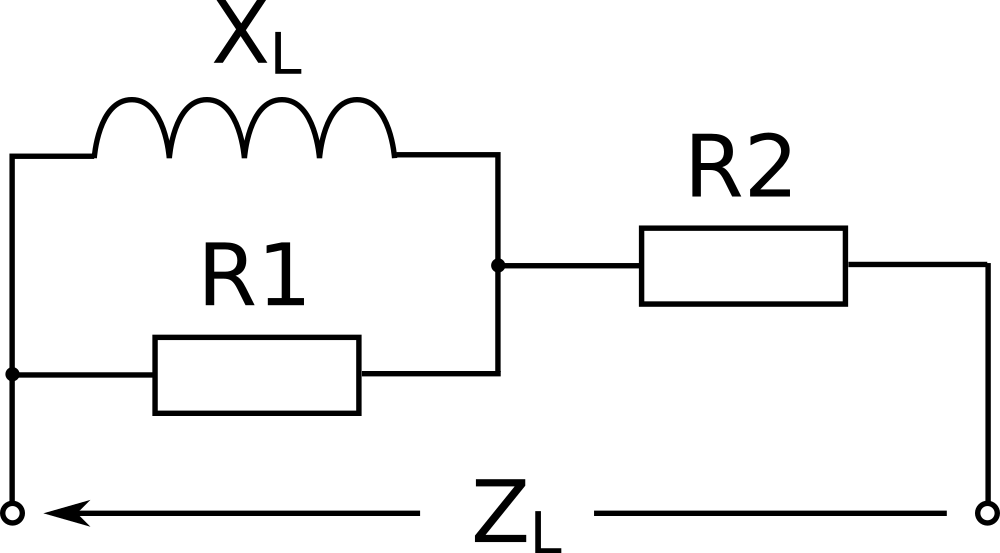
Das obige Ersatzschaltbild zeigt solche Dämpfungswiderstände für eine verlustbehaftete Spule. Um statt dessen ein Ersatzschaltbild für Kondensatoren zu erhalten, müssten lediglich XL und ZL gegen XC und ZC getauscht werden. Für viele Zwecke genügen Ersatzschaltbilder mit nur einem Dämpfungswiderstand, wo wir entweder R1→∞ oder R2=0 annehmen.

Um nun die Impedanzen ZC bzw. ZL verlustbehafteter realer Bauelemente zu messen, ist das Verständnis komplexer Zahlen zur Darstellung von Betrag und Phase von Wechselströmen und Wechselspannungen hilfreich. Wer sich mit komplexen Zeigerdiagrammen schwer tut, kann deren Bedeutung im Artikel zu Wechselströmen in der komplexen Zahlenebene nachlesen.

Versuchsaufbau zur Messung von Impedanzen

Für den Versuchsaufbau zum messen von Impedanzen benötigen wir folgende Ausrüstung: ein Zweikanal-Oszilloskop, einen Messgenerator bzw. Messsender, sowie eine Software zur Umrechnung und Auswertung der Ergebnisse. Zur Umrechnung kommt eine Tabellenkalkulation wie Excel oder LibreOffice in Frage. Mit statistischer Software wie R, Python oder Matlab lassen auch fortgeschrittenere Auswertungen realisieren.

Bei Digitaloszilloskopen mit Speicherung von Messdaten in Dateiformaten, welche direkt in Excel, R oder Matlab importiert werden können, vereinfacht sich die Auswertung erheblich. Die Schaltkreise zur Vermessung der Bauelemente bleiben jedoch gleich.

Die Messungen können in zwei Varianten erfolgen, von denen die erste den Stromfluss durch die Impedanz bestimmt und die zweite die an ihr abfallende Spannung. Variante 1 eignet sich besser für große Impedanzen und Variante 2 besser für kleine.

Variante 1: Messung über den Stromfluss

Bild 3 zeigt den Schaltkreis zur Messung von Impedanzen über den Stromfluss IL. Die beiden mit Spannungsteilern versehenen Kanäle des Oszilloskops erfassen das hochfrequente Eingangssignal U1 sowie die Sekundärspannung U2, aus welcher der Stromfluss IL durch die Spule folgt.

Zunächst einmal müssen den Kanälen des Oszilloskops Spannungsteiler vorgeschaltet werden, weil ansonsten die Kapazitäten der Messeingänge die Ergebnisse verfälschen würden. Bei einem Versuchsaufbau mit 50Ω Koaxialkabel bietet sich für den Parallelwiderstand R0 ein niedriger Wert um die 50Ω an, der sowohl den Leitungsimpedanzen entspricht als auch den Einfluss der parallel geschalteten Kapazität des Messeingangs verringert.

Um Verfälschungen durch Eingangskapazitäten weiter zu verringern, sollten zudem die Widerstände R1 und R2 deutlich größer als R0 sein. Es empfehlen sich dann Werte von mindestens 500Ω.

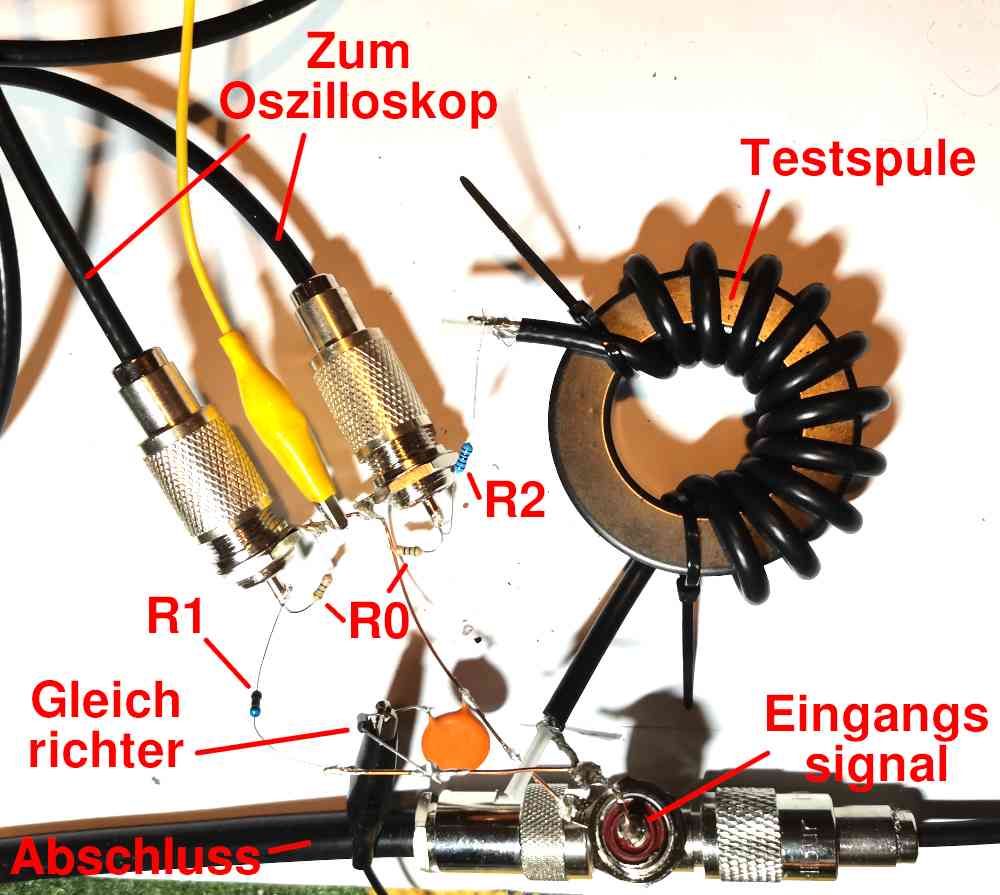
Bild 4 zeigt einen Versuchsaufbau entsprechend den Bauelementen des Schaltkreises in Bild 3. Zusätzlich ist noch ein optionaler Gleichrichter zur Messung der Amplitude des Eingangssignals eingebaut. Außerdem benötigt man zum Schutz des Messsenders einen 50Ω Abschlusswiderstand. Die Testspule ist mit Koaxialkabel gewickelt, weil im konkreten Experiment eine Mantelwellensperre vermessen wurde. Um bei Messung von hochfrequenten Signalen nicht die Phasen zu verfälschen, sollten die beiden Kabel zum Oszilloskop die gleiche Länge haben.

Messverfahren zur Variante 1

Wir messen über das Oszilloskop die Spannungen Uc1 und Uc2. Aus den Spannungsteilern R1/R0 und R2/R0 erhalten wir das Eingangssignal U1 sowie die Sekundärspannung U2. Der Strom IL durch das Bauelement folgt dann aus U2 und R2/R0:

U1 = Uc1 * (R1 + R0) / R0
U2 = Uc2 * (R2 + R0) / R0
IL = U2 / (R2 + R0)

Zur Impedanzmessung benötigen wir UL und IL. Während IL einfach zu messen ist, ergibt sich UL nur aus der Differenz von U1 und U2:

UL = U1 - U2

Wegen der Phasenverschiebungen im Schaltkreis kann die Differenzspannung UL aber nicht aus der Differenz der Amplituden bzw. Beträge der Spannungen U1 und U2 ermittelt werden!

|UL| ≠ |U1| - |U2|

Diesen Sachverhalt und die für unsere Impedanzmessung wichtigen Phasenverschiebungen erkennt man am besten in einem Zeigerdiagramm der komplexen Zahlenebene.

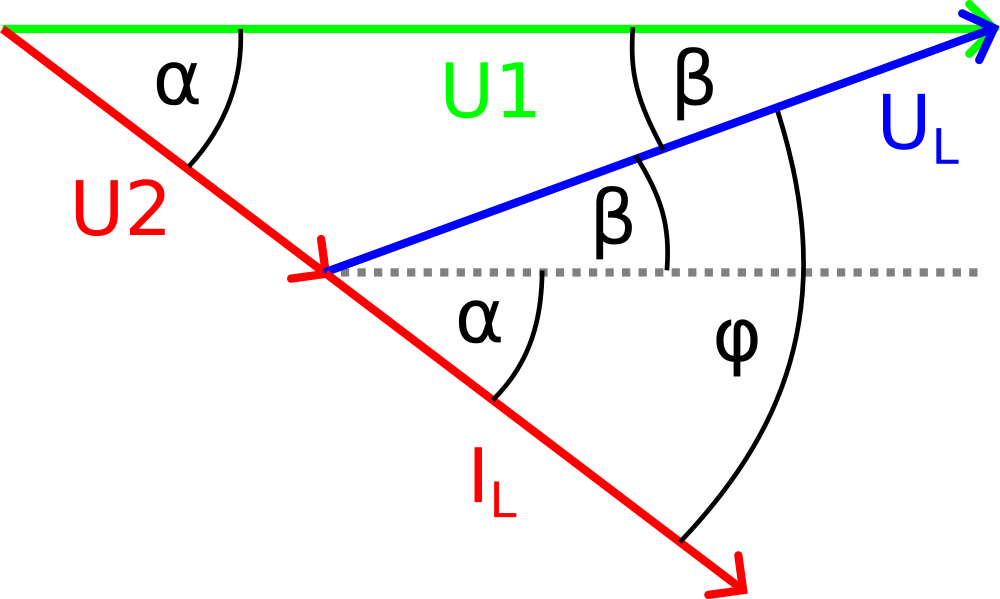
Wie in Bild 5 zu erkennen, eilen Spannung U2 und Strom IL der Eingangsspannung U1 um einen Phasenwinkel α nach. Die Spannung UL hingegen eilt der Eingangsspannung U1 um einen Winkel β voraus. Wie mittels der grau gepunkteten Linie parallel zu U1 angedeutet, addieren sich die Winkel α und β zur Phasenverschiebung φ zwischen IL und UL.

Für die Phasenverschiebung φ einer realen Spule und den Phasenwinkel α gilt: φ<90° und α<φ. Selbst bei einer idealen Spule ist die am Kanal 2 des Oszilloskops zu beobachtende Phasenverschiebung α also kleiner als 90°!

Die nachfolgenden Berechnungen beziehen sich jeweils auf die Vektorlängen bzw. Beträge der Spannungen und Ströme des Zeigerdiagramms. Der Einfachheit halber verzichte ich auf die Kennzeichnung von Beträgen, schreibe also beispielsweise UL statt |UL|.

Über die am Kanal 2 des Oszilloskops beobachtete Spannung U2 mit Phasenwinkel α können wir zunächst die Spannung UL berechnen. Mit dem Kosinussatz der Geometrie gilt:

UL2 = U12 + U22 - 2 * U1 * U2 * cos(α)
bzw.
UL = sqrt( U12 + U22 - 2 * U1 * U2 * cos(α) )

Aus UL folgt nun über die Umkehrung des Kosinussatzes der Winkel β:

β = arccos( (UL2 + U12 - U22)/(2 * U1 * UL) )

Aus der Trigonometrie des Diagramms der komplexen Zahlenebene haben wir nun alle Größen, die wir zur Berechnung der Impedanz ZL benötigen.

ZL = UL / IL
φ = α + β

ZL: Betrag der Impedanz der Spule
φ: Phasenverschiebung UL zu IL

Bei einer idealen Spule liegt der Winkel φ bei 90° und bei einer stark gedämpften Spule nähert er sich gegen 0°. Schließlich können wir noch die Werte von RL und XL des Ersatzschaltbildes errechnen.

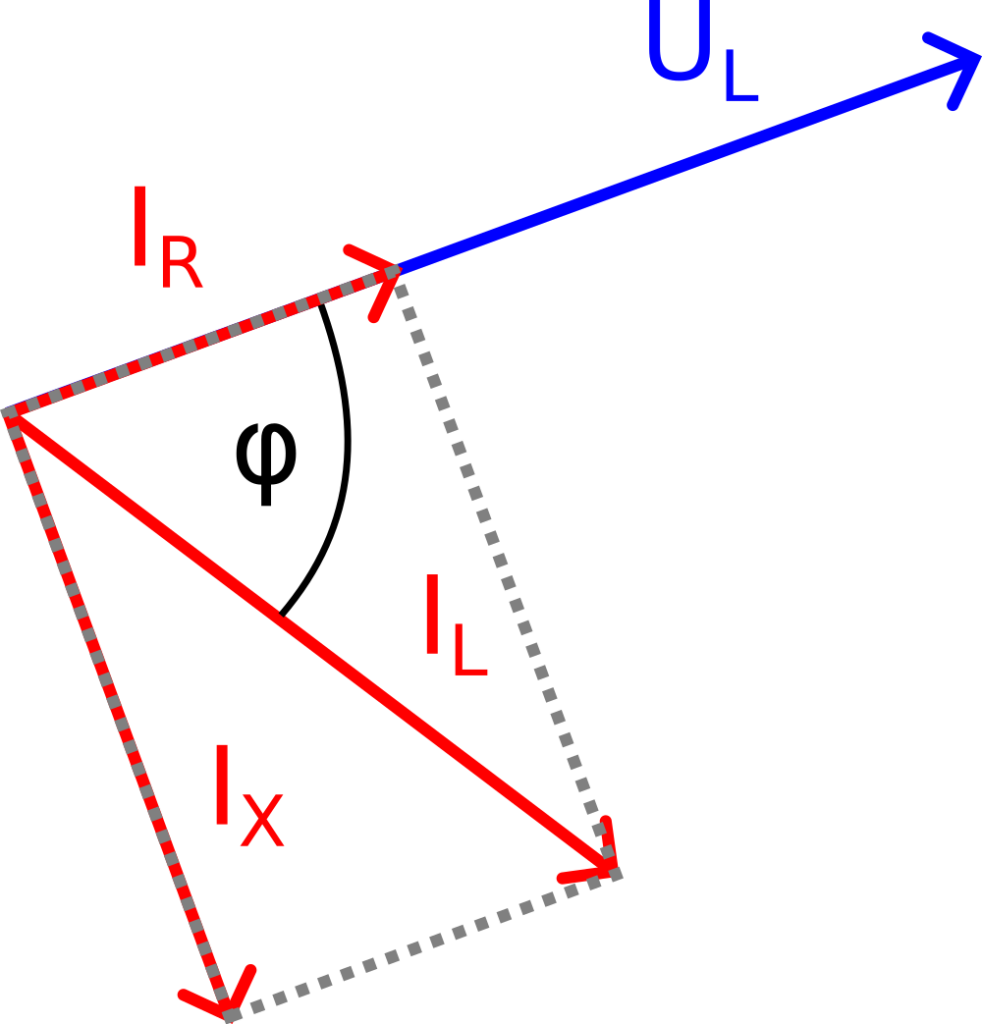
Weil wir im Ersatzschaltbild von einer Parallelschaltung des Realwiderstands RL und Blindwiderstands XL ausgegangen sind, suchen wir die Wirk- und Blindkomponenten des Stroms IL. Hierzu fügen wir wie in Bild 6 ein von IL aufgespanntes Rechteck ein. Somit gilt für die Stromkomponenten und Widerstände:

IR = IL * cos(φ)
IX = IL * sin(φ)
RL = UL / IR
XL = UL / IX

Zusammenfassung Variante 1 zur Messung von Impedanzen über den Stromfluss

Zusammengefasst ergibt sich die gesuchte Impedanz aus folgendem nichtlinearen Gleichungssystem:

U1 = Uc1 * (R1 + R0) / R0
U2 = Uc2 * (R2 + R0) / R0
IL = U2 / (R2 + R0)
UL = sqrt( U12 + U22 - 2 * U1 * U2 * cos(α) )
β = arccos( (UL2 + U12 - U22)/(2 * U1 * UL) )
ZL = UL / IL
φ = α + β
IR = IL * cos(φ)
IX = IL * sin(φ)
RL = UL / IR = ZL / cos(φ)
XL = UL / IX = ZL / sin(φ)

Eingangsvariablen:
Uc1: Signal am Kanal 1
Uc2: Signal am Kanal 2
α: Phasenverschiebung Uc1, Uc2
R0, R1, R2: Widerstände der Spannungsteiler

Ergebnisse:
ZL: Impedanz der Spule
φ: Winkel für den Wirkungsgrad
RL: Dämpfungswiderstand der Spule
XL: Blindwiderstand der Spule

Die Auflösung des Gleichungssystem erfolgt einfach in Excel. Ausgehend von den Eingangsvariablen können Zwischenergebnisse in separaten Spalten hinterlegt und anschließend in der nächsten Gleichung referenziert werden.

Variante 2: Messung über den Spannungsabfall

In Variante 2 des Versuchsaufbaus beobachten wir den Spannungsabfall UL an der Spule, müssen jedoch den Stromfluss IL zurück rechnen. Zunächst gilt für die Spannungen U1 und UL:

U1 = Uc1 * (R1 + R0) / R0
UL = Uc2 * (R2 + R0) / R0

Weiterhin bietet sich ein Ersatzschaltbild der Spule ZL sowie der Widerstände R1, R2 und R3 an:

Statt die gesuchte Impedanz ZL aus einer Parallelschaltung der Widerstände R2+R0 herausrechnen zu müssen, können wir den Spannungsteiler aus R3 und R2+R0 als eine ideale Spannungsquelle U1i mit Innenwiderstand R4 ansehen. Hierfür sind folgende Transformationen nötig:

U1i = U1 * (R2 + R0) / (R3 + R2 + R0)
R4 = (R2 + R0) * R3  / (R3 + R2 + R0)

Der Innenwiderstand R4 ist hierbei als Parallelschaltung der Widerstände R3 und R2+R0 errechnet. Mit der Ersatzschaltung nach Bild 8 ist der Stromfluss IL also:

U4 = U1i - UL
IL = U4 / R4

Wegen der Phasenverschiebungen im Schaltkreis kann die Spannung U4 jedoch nicht aus der Differenz der Beträge der Spannungen U1i und UL ermittelt werden.

|U4| ≠ |U1i| - |UL|

Hier ist wiederum ein Zeigerdiagramm der komplexen Zahlenebene hilfreich. Im Folgenden lasse ich die Kennzeichnung von Beträgen aus, schreibe also beispielsweise U4 statt |U4|.

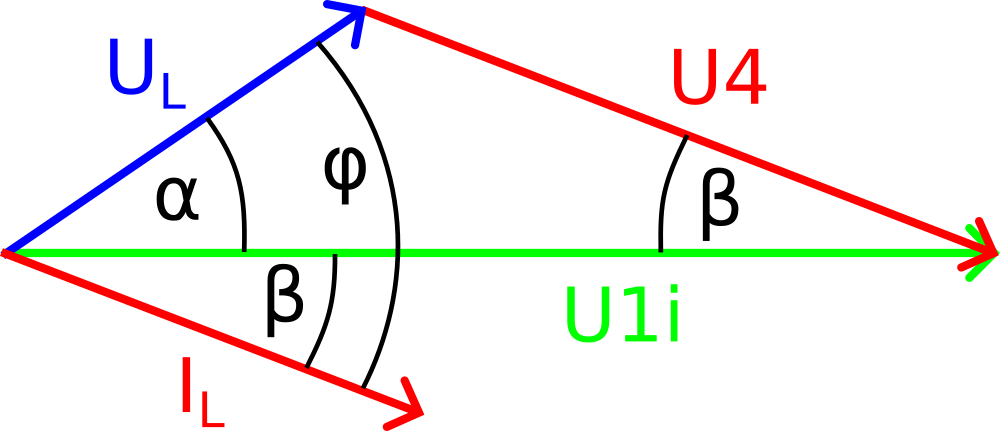
Erneut erhalten wir die Spannung U4 über die Phase α und den Kosinussatz.

U4 = sqrt( UL2 + U1i2 - 2 * UL * U1i * cos(α) )

Der Phasenwinkel β folgt nun aus U4 und der Umkehrung des Kosinussatzes.

β = arccos( (U42 + U1i2 - UL2)/(2 * U4 * U1i) )

Weil der Strom IL gleichphasig zum Spannungsabfall U4 an R4 verläuft, replizieren sich die Phasenwinkel β im Diagramm. Damit erhalten wir Betrag und Phase von IL:

IL = U4 / R4
φ = α + β

Analog zur Lösung für Variante 1 erhalten wir damit für Wirk- und Blindkomponenten der Impedanz ZL:

ZL = UL / IL
IR = IL * cos(φ)
IX = IL * sin(φ)
RL = UL / IR = ZL / cos(φ)
XL = UL / IX = ZL / sin(φ)

Zusammenfassung Variante 2 zur Messung von Impedanzen über den Spannungsabfall

Erneut erhalten wir als Zusammenfassung der Variante 2 ein nichtlineares Gleichungssystem zur Berechnung der gesuchten Impedanz ZL:

U1 = Uc1 * (R1 + R0) / R0
UL = Uc2 * (R2 + R0) / R0
U1i = U1 * (R2 + R0) / (R3 + R2 + R0)
R4 = (R2 + R0) * R3  / (R3 + R2 + R0)
U4 = sqrt( UL2 + U1i2 - 2 * UL * U1i * cos(α) )
β = arccos( (U42 + U1i2 - UL2)/(2 * U4 * U1i) )
IL = U4 / R4
φ = α + β
ZL = UL / IL
IR = IL * cos(φ)
IX = IL * sin(φ)
RL = UL / IR = ZL / cos(φ)
XL = UL / IX = ZL / sin(φ)

Eingangsvariablen:
Uc1: Signal am Kanal 1
Uc2: Signal am Kanal 2
α: Phasenverschiebung Uc1, Uc2
R0, R1, R2, R3: Widerstände der Spannungsteiler

Ergebnisse:
ZL: Impedanz der Spule
φ: Winkel für den Wirkungsgrad
RL: Dämpfungswiderstand der Spule
XL: Blindwiderstand der Spule

Auch in Variante 2 wird das Gleichungssystem in Excel gelöst. Wiederum kommen Zwischenergebnisse in separate Spalten, um sie in nachfolgenden Gleichungen zu referenzieren.

Referenzen

Kosinussatz: Wikipedia.org

Komplexe Wechselstromrechnung: Wikipedia.org

Ähnliche Inhalte

Impedanzen messen mit dem Oszilloskop auf Englisch: radiotechnologist.com