Wechselströme in der komplexen Zahlenebene

Zur vereinfachten Berechnung von Netzwerken mit Phasenverschiebungen durch Blindwiderstände bedient man sich gerne der komplexen Zahlen. Hierbei werden Wechselströme nach Betrag und Phase in der komplexen Zahlenebene dargestellt.

Gefolgt auf eine kurze mathematische Definition komplexer Zahlen erkläre ich die Abbildung von Cosinus-Funktionen in komplexen Zeigerdiagrammen. Als konkretes Beispiel werden anschließend Strom und Spannung einer idealen Spule im Zeigerdiagramm und zeitlichen Verlauf gegenübergestellt.

Komplexe Zahlen

Komplexe Zahlen haben Real- und Imaginärteile, die als Achsen die komplexe Zahlenebene aufspannen.

Z = a + i * b
mit i2 = -1

Z: komplexe Zahl
a: Realteil
b: Imaginärteil
i: die imaginäre Einheit

Der Imaginärteil ist hierbei eine gewöhnliche bzw. reelle Zahl, die mit der imaginären Einheit i2=-1 multipliziert wird. Weil es keine reelle Zahl gibt, die mit sich selbst multipliziert ein negatives Vorzeichen entwickelt, liegt also der Imaginärteil einer komplexen Zahl außerhalb der Menge der reellen Zahlen.

Wechselspannungen in Betrag und Phase

Komplexe Zahlen erleichtern es, Wechselspannungen in Betrag und Phase auszudrücken. Zur Überführung in die komplexe Zahlenebene wird beispielsweise einem Cosinus-Signal mit Spitzenwert Up

U = Up * cos(φ)

ein imaginäres Sinus-Signal i * sin(φ) hinzugefügt:

U = Up * ( cos(φ) + i * sin(φ) )

Up: Spitzenwert von U
cos(φ) + i * sin(φ): Phasenterm von U

Weil reelle und imaginäre Achsen senkrecht zueinander stehen, gilt für den Phasenterm der Satz des Pythagoras, wonach die Quadrate der reellen und imaginären Anteile das Quadrat des Betrags ergeben.

|cos(φ) + i * sin(φ)| = cos2(φ) + sin2(φ) = 1

Der Phasenterm hat also stets einen Betrag von eins, weswegen aus einem Cosinus mit Spitzenwert Up in der komplexen Zahlenebene ein rotierender Zeiger mit konstanter Länge U_p wird.

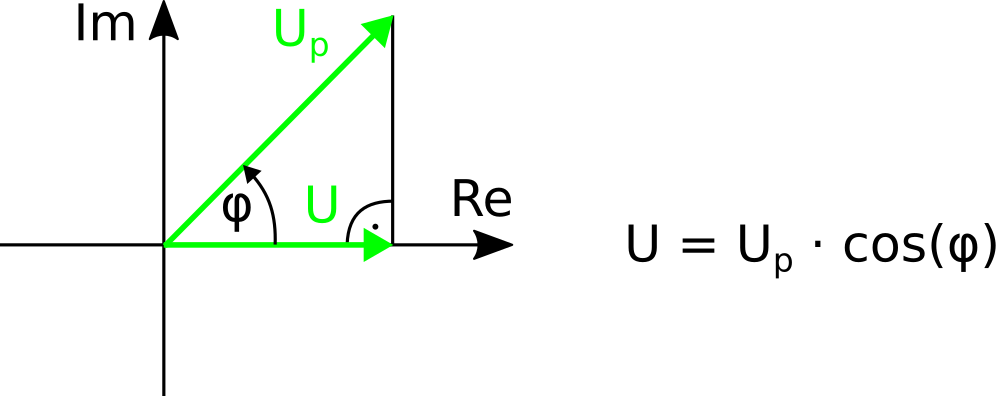
In einer Projektion auf die reelle Achse, wie sie in Bild 1 zu sehen ist, bleibt aber das ursprüngliche Signal erhalten. Beispielsweise hat der Zeiger U bei einem Phasenwinkel φ=0 die gleiche Länge wie Up, während er bei φ=90° verschwindet. Da jedoch die Zeigerlänge für Up konstant bleibt, also keine Nulldurchgänge durchläuft, erübrigt sich in der komplexen Zahlenebene die Rechnung mit Sinus und Cosinus.

Meistens wird in mathematischen Abhandlungen statt des Phasenterms mit Sinus und Cosinus die Exponentialfunktion mit imaginärem Exponenten verwendet.

cos(φ) + i * sin(φ) = eiφ
U = Up * eiφ

Beispiel: Strom und Spannung einer idealen Spule

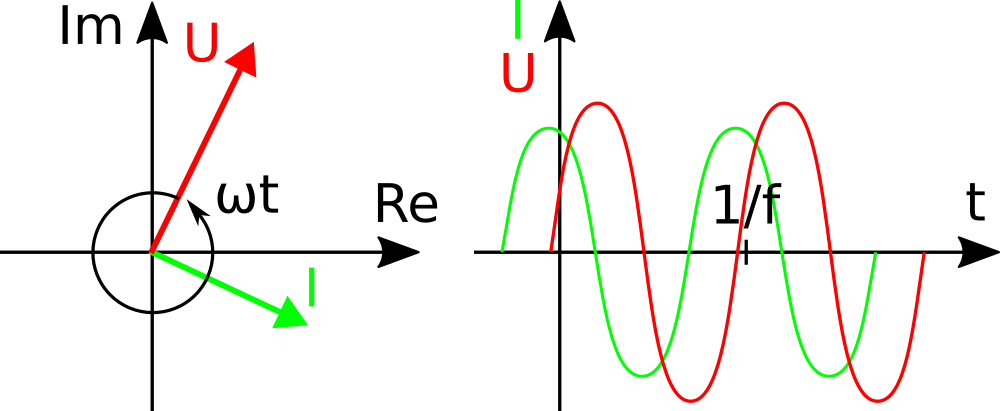
Bild 2 zeigt Strom und Spannung einer idealen Spule. Auf der linken Seite befinden sich die Zeiger der komplexen Zahlenebene und rechts die entsprechenden Signale im zeitlichen Verlauf. Links rotieren die Zeiger für Strom I und Spannung U mit Geschwindigkeit ω gegen den Uhrzeigersinn um den Schnittpunkt der imaginären und reellen Achsen der komplexen Zahlenebene. Rechts sehen wir die Sinuskurven aus der Projektion der Zeiger auf die reelle Achse.

Mit ω=2πf ist zum Zeitpunkt 1/f eine komplette Drehung von 2π bzw. 360° vollzogen, wobei f die Frequenz der Wechselsignale in Hertz ist. Links kehren die Zeiger nach vollen Drehungen an ihren ursprünglichen Ort zurück, während sich rechts die Zyklen der Sinuskurven ab der Markierung für t=1/f wiederholen. Zu jeder Zeit sind die realen Spannungen und Ströme die Projektionen der komplexen Zeiger auf die reelle Zahlenachse.

Der große Vorteil der Darstellung in der komplexen Zahlenebene ist es nun, einfach Vektoren aufaddieren zu können, anstatt mit Sinus und Cosinus in verschiedenen Phasen rechnen zu müssen. Im Artikel zur Messung von Impedanzen wird hiervon Gebrauch gemacht.

Referenzen

Satz des Pythagoras: Wikipedia.org

Komplexe Zahlen: Wikipedia.org

Komplexe Wechselstromrechnung: Wikipedia.org

Verwandte Themen

Wechselströme in der komplexen Zahlenebene auf Englisch: radiotechnologist.com.